Bài toán
Source: Codewars
Giới thiệu
Bất cứ nhóc Joey nào cũng biết bức ảnh này nghĩa là gì và tại sao nó là một nỗi đau (về mặt tâm lý TvT):

Trong nhiều trò chơi giải đố ma trận 2D, có một loại điển hình được gọi là ‘ice puzzle’:
- Bạn cần phải đi từ điểm A sang điểm B
- Bạn có thể di chuyển theo 1 trong 4 hướng trực giao
- Một vài ô sẽ có tính trơn: Nếu bạn bước vào ô trơn, bạn sẽ bị trượt trên hướng đang đi cho đến khi gặp một ô không trơn hoặc va chạm vào vật cản/tường.
Ví dụ, lời giải cho mê cung trên cùng bên trái của câu đố trên:
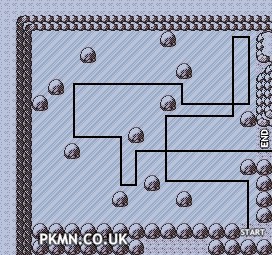
Đọc hiểu
Cho một hình chữ nhật kích thước M x N được chuẩn hóa theo dạng sau:
var map = '\
x \n\
# \n\
E \n\
# \n\
# \n\
S #';
/*
Người chơi xuất phát tại điểm bắt đầu và kết thúc khi đi đến ô kết thúc
S: ô bắt đầu (trơn, tồn tại duy nhất)
E: ô kết thúc (không trơn, tồn tại duy nhất)
: ô trơn
x: ô không trơn
#: vật cản
(Bạn khổng thể đi ra khỏi rìa của ma trận, nó đóng vai trò như các bức tường của câu đố.)
*/
Lời giải nên là tối ưu (số bước di chuyển là tối thiểu) và trả về mảng các hướng:'u', 'd', 'l', 'r' lần lượt là up/down/left/right. Ví dụ với mê cung trên, cần trả về ['u', 'r', 'd', 'l', 'u', 'r']. Nếu có nhiều lời giải với cùng số bước di chuyển, trả về lời giải với quãng đường đi ít nhất. Nếu vẫn bằng nhau, trả về bất cứ lời giải nào.
Thêm vào đó, trả về null cho qua một số mê cung không có lời giải thích hợp.
Lời giải
Mê cung đọc vào ở dạng chuỗi, sử dụng đồ thị thì rối với tính chất của mê cung, mình cũng lười đưa nó về ma trận nên để vậy tính luôn. 
Lấy mê cung sau làm ví dụ:
" x \n"
" # \n"
" E \n"
" # \n"
" # \n"
"S #"
Nếu xem chuỗi mê cung là một ma trận, vậy số cột col của nó là vị trí của '\n' + 1 và là một ma trận đánh số bắt đầu từ 0.
Dễ thấy, nếu ô hiện tại ở vị trí i thì vị trí của 4 ô liền kề lần lượt là:
- Ô bên trên:
i - col - Ô bên dưới:
i + col - Ô bên trái:
i - 1 - Ô bên phải:
i + 1
Như vậy, để tìm được đích đến của một bước di chuyển nào mình dùng vòng lặp như sau:
#define UP 0
#define DOWN 1
#define LEFT 2
#define RIGHT 3
int next_tile(const std::string &map, int col, int curr, char dir) {
int row = (map.length() + 1) / col;
while (map[curr] != 'E' && is_valid(curr, dir, col, row)) {
int next;
switch (dir) {
case UP: next = curr - col; break;
case DOWN: next = curr + col; break;
case LEFT: next = curr - 1; break;
default: next = curr + 1; break;
}
if (map[next] == '#')
return curr;
if (map[next] == 'x')
return next;
curr = next;
}
return curr;
}
Hàm is_valid dùng để đảm bảo việc di chuyển không vượt qua khỏi phạm vi mê cung
bool is_valid(int pos, char dir, int col, int row) {
switch (dir) {
case UP: return pos >= col;
case DOWN: return pos <= col * (row - 1) - 1;
case LEFT: return pos % col != 0;
}
return (pos - col + 2) % col != 0;
}
Thuật toán chính cho bài này là tìm kiếm theo chiều rộng (tìm kiếm theo chiều sâu vẫn khả thi, nhưng nó không thực sự hiệu quả đối với các map lớn). Mỗi khi xét một ô, xác định đích đến (next) của 4 hướng xung quanh rồi cho vào hàng đợi. Có 2 trường hợp sẽ xảy ra: tồn tại một đường đi khác đến next và ngược lại.
Nếu tồn tại một đường đi khác, next sẽ không được thêm vào hàng đợi mà đường đi đến next sẽ được cập nhật lại sao cho lời giải sau cùng là tối ưu. Khởi tạo mảng precell lưu trữ ô trước đó, mặc định tất cả các ô là -1, hỗ trợ việc truy vết đường đi từ start đến một ô bất kỳ.
Ngoài ra, cần phải lưu ý tránh thêm ô xuất phát vào hàng đợi, gây vô hạn lặp.
std::vector<char> ice_maze_solver(const std::string &map) {
int col = map.find("\n") + 1, start = map.find("S"), end = map.find("E");
bool solvable = false;
std::vector<char> solution;
std::vector<int> precell(map.length(), -1);
std::queue<int> queue;
queue.push(start);
while (!queue.empty()) {
int curr = queue.front();
queue.pop();
if(curr == end){
solvable = true;
continue;
}
for (int i = 0; i < 4; i++) {
int next = next_tile(map, col, curr, i);
if (next != curr && next != precell[curr]) {
if(precell[next] != -1){
update_path(precell, col, curr, next);
}
else if (next != start){
precell[next] = curr;
queue.push(next);
}
}
}
}
if (solvable){
while (end != start) {
char move;
if ((precell[end] - end) % col == 0)
move = (precell[end] > end) ? 'u' : 'd';
else
move = (precell[end] > end) ? 'l' : 'r';
solution.insert(solution.begin(), move);
end = precell[end];
}
}
return solution;
}
Đường đi được cập nhật thông qua 2 yếu tố:
- Số bước di chuyển
- Tổng độ dài của đường đi, trong đó:
- Khoảng cách của 2 ô $i, j$ bất kỳ trên cùng một hàng ngang được tính bằng $|i-j|$
- Nếu 2 ô trên cùng hàng dọc: $\dfrac{|i-j|}{col}$
std::vector<int> get_length(
std::vector<int> const &parent, const int col, int curr) {
int length = 0;
int step = 0;
while (parent[curr] != -1) {
step++;
length += abs(parent[curr] - curr) / ((parent[curr] - curr) % col == 0 ? col : 1);
curr = parent[curr];
}
return {step, length};
}
void update_path(std::vector<int> &parent, const int col, int curr, int next) {
auto oldPath = get_length(parent, col, next);
auto newPath = get_length(parent, col, curr);
newPath[0] += 1;
newPath[1] += abs(curr - next) / ((curr - next) % col == 0 ? col : 1);
if (newPath < oldPath) {
parent[next] = curr;
}
}
Cảm ơn bạn vì đã đọc vì cái lời giải này nó nghiệp dư vô cùng, và mình “đấm” cái kata này vì nó có liên quan tới pokemon thôi.
