Problem

Any youngster Joeys should probably know what this image means, and why it is traumatic:

IcePath-1F-GS

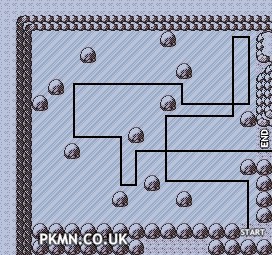
In many grid-based 2D puzzle games, there is a typical form of puzzle which are usually referred to as ‘ice puzzle’:

You have to traverse from point A to point B
You can move towards one of the 4 orthogonal directions, 1 tile at a time
Some of the floors are slippery; if you walk onto a slippery tile, you’ll keep sliding in the direction you’re going until you land on a non-slippery tile, or you collide with an obstacle/wall

For example, the top-left part of the above puzzle has such a solution:

IcePathSolution

You will be given an M x N well-formed rectanglar ASCII map of the form:

var map = '\
    x \n\
  #   \n\
   E  \n\
 #    \n\
    # \n\
S    #';
/*
Player starts at the start, and ends by reaching the end.

legend: 
S: start (slippery, only 1 exists)
E: end (non-slippery, only 1 exists)
 : slippery tile
x: non-slippery tile
#: obstacles
(You can't go past map edges, which serves as the walls of the puzzle.)
*/

Your solver should find the optimal solution (minimal number of moves, as in, the amount of times you make a step), and return an array of directions: 'u', 'd', 'l', 'r' for up/down/left/right respectively. So for the example map above, you should return ['u', 'r', 'd', 'l', 'u', 'r']. If there are multiple solutions with the same amount of steps, tiebreak by least distance traversed. If there are still ties, just return any one of them.

Also, you might be passed some maps which does not admit any solutions. In this case, return null.

Solution

The maze is read as a string, using graph hurts my brain as well as I’m too lazy to transform it into matrix so, let it be.

As an example:

"    x \n"
"  #   \n"
"   E  \n"
" #    \n"
"    # \n"
"S    #"

Consider this maze as a matrix, it’s columns equal to position of '\n' + 1 besides, this is a numbered matrix, starts from 0.

Conspicuously, if current cell is at position i, it’s 4 adjacent cells would be:

Upper cell: i - col
Lower cell: i + col
Left cell: i - 1
Right cecll: i + 1

Thus, a while loop is used to find a move’s destination:

#define UP    0
#define DOWN  1
#define LEFT  2
#define RIGHT 3

int next_tile(const std::string &map, int col, int curr, char dir) {
    int row = (map.length() + 1) / col;
    while (map[curr] != 'E' && is_valid(curr, dir, col, row)) {
        int next;
        switch (dir) {
        case UP:   next = curr - col; break;
        case DOWN: next = curr + col; break;
        case LEFT: next = curr - 1;   break;
        default:   next = curr + 1;   break;
        }
        if (map[next] == '#')
            return curr;
        if (map[next] == 'x')
            return next;
        curr = next;
    }
    return curr;
}

is_valid function is responsible for ensuring the movement doesn’t go out of the maze’s walls

bool is_valid(int pos, char dir, int col, int row) {
    switch (dir) {
        case UP:   return pos >= col;
        case DOWN: return pos <= col * (row - 1) - 1;
        case LEFT: return pos % col != 0;
    }
    return (pos - col + 2) % col != 0;
}

The main algorithm for this kata is breadth first search (depth first search is possible, however, it can not take care of the bigger maze). When traverse a cell, calculate it’s destinations (next) for each of 4 directions, then push them to queue. There are 2 case would occur: There is another path which leads to next and there is none.

If another path exists, next would not be pushed to queue but its path would be updated so that the solution is an optimal one. Init precell array to store cells’ previous cell, -1 as default, to supports tracing back a path from start to any cell.

Moreover, pay attention to avoid adding start cell into queue, which causes infinite loop.

std::vector<char> ice_maze_solver(const std::string &map) {
    int col = map.find("\n") + 1, start = map.find("S"), end = map.find("E");
    bool solvable = false;
    std::vector<char> solution;
    std::vector<int> precell(map.length(), -1);
    
    std::queue<int> queue;
    queue.push(start);
    
    while (!queue.empty()) {
        int curr = queue.front();
        queue.pop();
        if(curr == end){
            solvable = true;
            continue;
        }
        for (int i = 0; i < 4; i++) {
            int next = next_tile(map, col, curr, i);
            if (next != curr && next != precell[curr]) {
                if(precell[next] != -1){
                    update_path(precell, col, curr, next);
                }
                else if (next != start){
                    precell[next] = curr;
                    queue.push(next);
                }
            }
        }
    }
    
    if (solvable){
        while (end != start) {
            char move;
            if ((precell[end] - end) % col == 0)
                move = (precell[end] > end) ? 'u' : 'd';
            else
                move = (precell[end] > end) ? 'l' : 'r';
            solution.insert(solution.begin(), move);
            end = precell[end];
        }
    }
    return solution;
}

The path is updated through 2 factors:

Number of steps
Total path length, where:
- The distance between 2 cells in the same horizontal row is $|i-j|$
- If they’re in the same vertical row: $\dfrac{|i-j|}{col}$

std::vector<int> get_length(
    std::vector<int> const &parent, const int col, int curr) {
    int length = 0;
    int step   = 0;
    while (parent[curr] != -1) {
        step++;
        length += abs(parent[curr] - curr) / ((parent[curr] - curr) % col == 0 ? col : 1);
        curr = parent[curr];
    }
    return {step, length};
}

void update_path(std::vector<int> &parent, const int col, int curr, int next) {
    auto oldPath = get_length(parent, col, next);
    auto newPath = get_length(parent, col, curr);
    newPath[0] += 1;
    newPath[1] += abs(curr - next) / ((curr - next) % col == 0 ? col : 1);
    if (newPath < oldPath) {
        parent[next] = curr;
    }
}

Thank you for reading this amateur solution, I did this kata just because it is related to pokemon series, nothing else.

rowlet

Problem#

Solution#

Problem

Solution